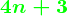三つ子素数

三つ子素数（みつごそすう、prime triplet）もしくは三つ組素数とは、3個の素数の組で、(p, p 2, p 6) または (p, p 4, p 6) のタイプのもののことである。

概要

三つ子素数は双子素数、いとこ素数、セクシー素数を含む。

なお、双子素数は「2つの素数の組 (p, p 2)」と定義されるのに対し、3つの素数の組である三つ子素数を「(p, p 2, p 4)」と定義していない。

この形は (3, 5, 7) のみであるからと、p が5以上の素数の場合、「(p 2, p 4)」のいずれかが必ず3の倍数になるからである。

三つ子素数を小さい順に並べると、次のようになる。

(5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (17, 19, 23), (37, 41, 43), (41, 43, 47), (67, 71, 73), (97, 101, 103), …

三つ組の中で最小の素数のみを並べると、

5, 7, 11, 13, 17, 37, 41, 67, 97, 101, 103, 107, 191, 193, 223, 227, 277, 307, 311, 347, 457, 461, 613, 641, 821, 823, 853, 857, 877, 881, 1087, …（オンライン整数列大辞典の数列 A7529）

である。このうち、(p, p 2, p 6) のタイプのものは

5, 11, 17, 41, 101, 107, 191, 227, 311, 347, 461, 641, 821, 857, 881, … (A22004)

(p, p 4, p 6) のタイプのものは

7, 13, 37, 67, 97, 103, 193, 223, 277, 307, 457, 613, 823, 853, 877, 1087, … (A22005)

となる。

予想

三つ子素数は無数に存在すると予想されている。ハーディとリトルウッドはより詳細な予想を立てており、それによると、x 未満の (p, p 2, p 6) の形の三つ子素数、(p, p 4, p 6) の形の三つ子素数のそれぞれの個数はおよそ

{\frac {9}{2}}\prod _{p\geq 5}{\frac {p^{2}(p-3)}{(p-1)^{3}}}\int _{2}^{x}{\frac {dx}{(\log x)^{3}}}\approx 2.858248596\int _{2}^{x}{\frac {dx}{(\log x)^{3}}}

であるらしい。10⁸ 未満の三つ子素数の個数は、それぞれ 55,600 と 55,556 であり、上記推定値は 55,490 である。

知られている三つ子素数で最大の p は、(p, p 2, p 6) の形では2019年4月に発見された20008桁の 4111286921397 × 2⁶⁶⁴²⁰ − 1 であり、(p, p 4, p 6) の形では2013年4月に発見された16737桁の 6521953289619 × 2⁵⁵⁵⁵⁵ − 5 である。